
Music Player
CADASTRE-SE
Seja Nosso MEMBRO!
Sua Doação nos ajudará a manter esta Revista.
Nosso PIX:
375.234.149-15
Obrigado!
Temos Uma versão desta Revista Especificamente para SmartPhone
Mais Enxuta: Somente Vídeo Aulas e EVENTOS!
l


MATEMÁTICA
Disciplina: Geometria Descritiva

Tipos de Reta
(Exercícios Resolvidos)
Representação de Retas em Perspectiva e em Épora:
1) Reta Qualquer;
2) Reta Horizontal;
3) Reta Frontal;
4) Reta de Topo;
5) Reta Vertical;
6) Reta Fronto-Horizontal; e
7) Reta de Perfil.
Tipos de Retas:
1) Reta Qualquer: É aquela reta q que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - a qual intercepta os dois Planos Vertical π2 e Plano Horizontal π1 os quais formam os Diedros (os quatro lugares cujos lados são formados pelos Planos Vertical e Horizontal perpendiculares entre si). Adotaremos a Perspectiva Isométria¹ ou próxima dela! Pontos, Retas e Planos sempre desenhados no 1o. Diedro², com exceções nos exercícios onde na solução do mesmo resulte uma Ponto ou Reta ou Plano com projeções que apareçam em Diedros diferentes 2o., 3o. e/ou 4o. Em Épura, com respeito à Reta q temos a Projeção Vertical q2 e a Projeção Horizontal q1 são ambas Oblíquas à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal). Os Planos Plano Vertical π2 e Plano Horizontal π1 são chamados de Planos de Projeção.
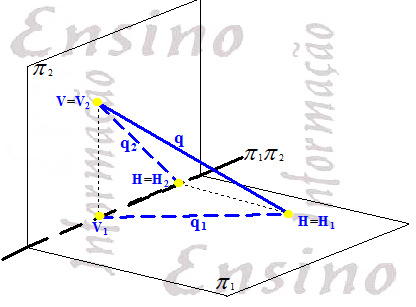

Tipos de Retas:
2) Reta Horizontal: É aquela reta h que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - a qual intercepta o Plano Vertical π2 e é Paralela ao Plano Horizontal π1. Em Épura, com respeito à Reta h temos a Projeção Vertical h2 Paralela à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal) e a Projeção Horizontal h1 Oblíqua à Linha de Terra.


Tipos de Retas:
3) Reta Frontal: É aquela reta f que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - a qual intercepta o Plano Horizontal π1 e é Paralela ao Plano Vertical π2. Em Épura, com respeito à Reta f temos a Projeção Horizontal f1 Paralela à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal) e a Projeção Vertical f2 Oblíqua à Linha de Terra.


Tipos de Retas:
4) Reta Fronto-Horizontal: É aquela reta fh que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - é Paralela ao Plano Vertical π2 e ao Plano Horizontal π1. Em Épura, com respeito à Reta fh temos a Projeção Horizontal fh1 Paralela à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal) e a Projeção Vertical fh2 Paralela, também, à Linha de Terra.


Tipos de Retas:
5) Reta de Topo: É aquela reta t que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - é Paralela ao Plano Horizontal π1 e Perpendicular ao Plano Vertical π2 no Ponto V. Em Épura, com respeito à Reta t temos a Projeção Horizontal t1 Perpendicular à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal) e a Projeção Vertical t2 se reduz a um Ponto V no Plano Vertical π2. OBSERVAÇÃO: Isto considerando a Reta t localizada (parte dela) no 1o. Diedro, como mostram as Figuras abaixo!


Tipos de Retas:
6) Reta Vertical: É aquela reta v que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - é Paralela ao Plano Horizontal π2 e Perpendicular ao Plano Vertical π1 no Ponto H. Em Épura, com respeito à Reta v temos a Projeção Vertical v2 Perpendicular à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal) e a Projeção Horizontal v1 se reduz a um Ponto H no Plano Horizontal π1. OBSERVAÇÃO: Isto considerando a Reta v localizada (parte dela) no 1o. Diedro, como mostram as Figuras abaixo!


Tipos de Retas:
7) Reta de Perfil: É aquela reta p que no Espaço Tridimensional - Espaço Euclidiano R³ com pontos M de Coordenadas M=(x, y , z) com x, y e z Números Reais - é Oblíqua ao Plano Horizontal π2 no Ponto V e Oblíqua ao Plano Vertical π1 no Ponto H. e esta Reta P está contida no Plano φ o qual é Perpendicular, ao mesmo temo, aos Planos π1 e π2. Em Épura, com respeito à Reta p temos a Projeção Vertical p2 Perpendicular à Linha de Terra π1π2 (é a interseção dos Plano Vertical e Plano Horizontal) e a Projeção Horizontal p1 Perpendicular, também, à Linha de Terra π1π2. OBSERVAÇÃO: Isto considerando a Reta p localizada (parte dela) no 1o. Diedro, como mostram as Figuras abaixo! OBSERVAÇÃO: Esta é a única Reta dentre as 07 demais Retas a qual é necessário dar dois Ponto A e B para bem defini-la haja vista que o Observador olhando de Frente para o Plano Vertical π2, mesmo com os dois pontos A e B dados, não consegue saber sua INCLINAÇÃO (tanto com respeito ao Plano π1 e ao Plano π1) - temos que olhar esta reta vista de PERFIL, ou seja, o Observador agora olhando de Frente para o Plano φ... Esta nova maneira de ver de Perfil a reta p será obtida (veremos em outra oportunidade) fazendo o REBATIMENTO da Reta p no Plano π2 (ou em outro contexto, faremos uma MUDANÇA DE PLANO VERTICAL o π2 para obter o mesmo resultado, ou equivalente, saber exatamente o comprimento do Segmento de Reta AB!).


UM RESUMO DAS 07 RETAS VISTAS ACIMA

__________________________________________
(1) Perspectiva isométrica:
Quando olhamos para um objeto, temos a sensação de profundidade e relevo. As partes que estão mais próximas de nós parecem maiores e as partes mais distantes aparentam serem menores. A fotografia mostra um objeto do mesmo modo como ele é visto pelo olho humano, pois transmite a idéia de três dimensões: comprimento, largura e altura. O desenho, para transmitir essa idéia, precisa recorrer a um modo especial de representação: a perspectiva. Ela representa graficamente as três dimensões de um objeto em um único plano, de maneira a transmitir a idéia de profundidade e relevo. Existem diferentes tipos de perspectiva. Veja como fica a representação de um cubo em três tipos de perspectiva:
Cada tipo de perspectiva mostra o objeto de um jeito. Comparando as três formas de representação, você pode notar que a perspectiva isométrica é a que dá ideia menos deformada do objeto. Isso quer dizer que, usando-se mesma Métrica (Medida), a Perspectiva Isométrica mantém as mesmas proporções do comprimento, da largura e da altura do objeto representado. Além disso, o traçado da perspectiva isométrica é relativamente simples. Por essas razões, neste contexto da Geometria Descritiva nos utilizaremos da Perspectiva Isométrica para a Representação Espacial em R³ dos elementos: Ponto; Reta e Plano. Ver Figura abaixo!


Figura: Perspectiva Isométria
Uma Leitura Suplementar sobre Perspectiva Isométrica:
a) Perspectiva (gráfica) - Wikipédia
b) Desenhando Perspectiva Isométrica - Arquivo no Formato ".PDF"
c) Vídeo sobre perspectiva Isométrica
___________________________________________
(2) Diedro: Em Geometria, diedro, ângulo diedro ou ângulo diédrico é uma expansão do conceito de ângulo a um espaço tridimensional. É definido como o espaço entre dois semiplanos não contidos num mesmo plano com origem numa aresta comum. Continuar a Leitura em Wikipédia (Diedros) onde pode-se ver que os planos não precisam ser Perpendiculares em si para se ter um Diedro que é, não querendo sermos prolíxos, a parte entre dois lados formados por dois planos. Já o Triedro é parte formada por três lados - Ver Formato ".PDF"!
A partir de 14 Set de 2020
Você é o Visitante de Número




